Skip to main content

Measures of Central Tendency

Image
By itsRashad
Central Tendency: - The tendency of the individual item of a statistical series to cluster around the central value is called the Central Tendency. Sometimes it is called the measure of location or a measure of representation.

Several types of Central Tendency can be defined: The commons are

  1. The Arithmetic Mean
  2. The Median
  3. The Mode
  4. The Geometric Mean
  5. The Harmonic Mean

The Arithmetic Mean: - The Arithmetic Mean of a grouped frequency distribution is defined as


A = any guessed or assumed class mark.

f = Frequency of each class interval.

n = Sum of total frequency.

i = Range of class interval.

d = Deviation of the assumed class mark from each class interval by the range of class interval.

d = (Xi – A) / i

The Median: - The Median of a grouped is defined as




Where,

Me = Median of the total class.

fc = Previous cumulative frequency of all classes above the media class.

fm = Frequency of the corresponding class interval.

i = range of class interval.

L = Lower class boundary of median class.

n = Sum of total frequency.

The Mode: - The Mode of a set of number is that value which occurs with the greatest frequency.

The Mode for a grouped data/frequency distribution is denoted by




Where,

L = Lower limit of modal class interval.

∆1 = Difference between modal and pre-modal group.

∆2 = Difference between modal and post-modal group

i = range of class interval.

The Geometric Mean: - The Geometric Mean is for a grouped frequency distribution is denoted by




Where,

G = Geometric Mean

n = sum of total frequency.

fi = Frequency corresponding each class interval.

xi = Class Mark.

The Harmonic Mean: - The Harmonic Mean H for a grouped frequency distribution is




Where,

H = Harmonic Mean.

n = sum of total frequency.

fi = Frequency corresponding each class interval.

xi = Class Mark.

Problem: -

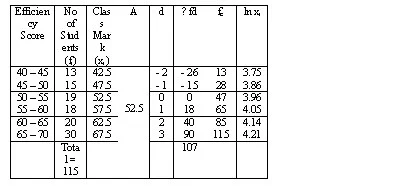
The given frequency is the efficiency score of 115 students in their 70% marks. Find the Arithmetic Mean, Median, Mode, Geometric Mean and Harmonic Mean.

Solution:

Justify Full






Some special measurements following any section of Central Tendency:

  1. Quartiles
  2. Deciles and
  3. Percentile

Quartiles: - The Quartiles are those values in a series which divide the total frequency into four equal parts. It is denoted by Q where

Where,

r = 1, 2, 3,…….

Lr = Lower limit of the Quartiles class,

n = Sum of the total frequency,

r = Position of Quartiles,

Fr = Cumulative frequency of the pre-rth Quartiles class,

fr = Corresponding frequency,

i = Range of class interval.

Deciles: - The Deciles are those values in a series which divide the total frequency into ten equal parts. It is denoted by D where

Where,

r = 1, 2, 3,…….

Lr = Lower limit of the Deciles class,

n = Sum of the total frequency,

r = Position of Deciles,

Fr = Cumulative frequency of the pre-rth Deciles class,

fr = Corresponding frequency,

i = Range of class interval.

Percentiles: - The Percentiles are those values in a series which divide the total frequency into 100 equal parts. It is denoted by P where




Where,

r = 1, 2, 3,…….

Lr = Lower limit of the Percentiles class,

n = Sum of the total frequency,

r = Position of Percentiles,

Fr = Cumulative frequency of the pre-rth Percentiles class,

fr = Corresponding frequency,

i = Range of class interval.

Labels:

Comments

Post a Comment

Popular Posts

Graphical Distribution of Frequency Distribution

By itsRashad
Frequency distribution can be presented graphically in any one of the following ways: Histogram Frequency Polygon Smooth Frequency Curve Cumulative Frequency Curve of Ogive Curve Pie-Chart Histogram: - A histogram is an area diagram in which the frequencies corresponding to each class interval of frequency distribution are by the area of a rectangle without leaving no gap between the cosective rectangles. Frequency Polygon: - This is one kind of histogram which is represented by joining the straight lines of the mid points of the upper horizontal side of each rectangle with adjacent rectangles. Smooth Frequency Curve: - This is one kind of histogram which is represented by joining the mid points by free hand of the upper horizontal side of each rectangle with adjacent rectangles. Comulative Frequency Curve or Ogive Curve: - The total frequency of all values less then the upper class boundary of a...
Post a Comment
Read more

Empirical Relation between Mean, Median and Mode

By itsRashad
A distribution in which the values of mean, median and mode coincide (i.e. mean = median = mode) is known as a symmetrical distribution. Conversely, when values of mean, median and mode are not equal the distribution is known as asymmetrical or skewed distribution. In moderately skewed or asymmetrical distribution a very important relationship exists among these three measures of central tendency. In such distributions the distance between the mean and median is about one-third of the distance between the mean and mode, as will be clear from the diagrams 1 and 2 Karl Pearson expressed this relationship as:
1 comment
Read more

Correlation and Linearity

By itsRashad
Correlation coefficients measure the strength of association between two variables. The most common correlation coefficient, called the Pearson product-moment correlation coefficient , measures the strength of the linear association between variables. In this tutorial, when we speak simply of a correlation coefficient, we are referring to the Pearson product-moment correlation. Generally, the correlation coefficient of a sample is denoted by r , and the correlation coefficient of a population is denoted by ρ or R . How to Interpret a Correlation Coefficient The sign and the absolute value of a correlation coefficient describe the direction and the magnitude of the relationship between two variables. The value of a correlation coefficient ranges between -1 and 1. The greater the absolute value of a correlation coefficient, the stronger the linear relationship. The str...
Post a Comment
Read more

Poisson Distribution

By itsRashad
A Poisson experiment is a statistical experiment that has the following properties: The experiment results in outcomes that can be classified as successes or failures. The average number of successes (μ) that occurs in a specified region is known. The probability that a success will occur is proportional to the size of the region. The probability that a success will occur in an extremely small region is virtually zero. Note that the specified region could take many forms. For instance, it could be a length, an area, a volume, a period of time, etc. Notation The following notation is helpful, when we talk about the Poisson distribution. e : A constant equal to approximately 2.71828. (Actually, e is the base of the natural logarithm system.) μ: The mean number of successes that occur in a specified region. x : The actual number of successes that occur in a specified region. P( x ; μ): The Poisson probability that exactly x ...
Post a Comment
Read more